Overview
This tutorial describes the theory of operation of the hydrodynamics plugin. It's heavily based on [3], and we recommend to read the full paper for a deeper understanding of its theory.
Understanding Hydrodynamic Forces
The behavior of a moving body through water is different from the behavior of a ground based vehicle. In particular bodies moving underwater experience much more forces derived from drag, buoyancy and lift. The way these forces act on a body can be seen in the following diagram:
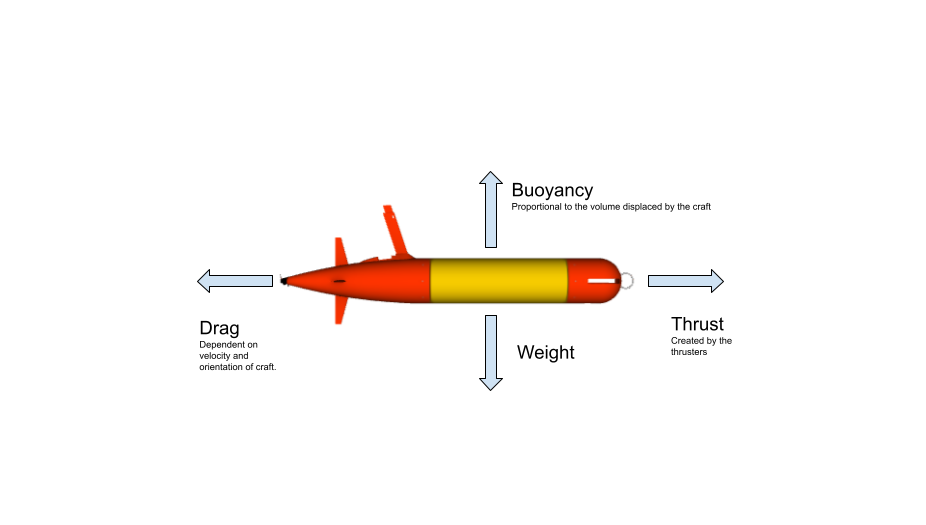
The hydrodynamics plugin
To approximate the motion of the vehicle in the ocean environment, we adapt Fossen’s six degree-of-freedom robot-like vectorial model for marine craft [2] expressed as
$$M ẍ + D(ẋ)ẋ + C(ẋ)ẋ = F$$
where M is the added mass matrix, D(ẋ) is the damping matrix, C(ẋ) is the Coriolis matrix, and ẋ is the velocity six-vector.
If present, ocean current is approximated by adding a term vc to the velocity:
$$M ẍ + D(ẋ − vc )(ẋ − vc ) + C(ẋ − vc )(ẋ − vc ) = F$$
The hydrodynamic forces include the added mass terms due to inertia of the surrounding fluid, the Coriolis-centripetal matrix for the added mass, and hydrodynamic damping. The hydrodynamic damping includes forces due to radiation-induced potential damping, skin friction, wave drift damping, vortex shedding and lifting forces. These effects are aggregated in the hydrodynamic damping matrix. This approximation of the hydrodynamic effects is implemented in this Gazebo plugin. The user defines the characteristics of the vessel under test through a vessel-specific configuration that includes the hydrodynamic derivatives. During each time step of the simulation, the plugin is executed with access to the state of the vessel and environment. The hydrodynamic force terms are calculated based on this state information and the user-defined vessel characteristics. The resulting force and moment values are then applied to the vessel through the Gazebo API for inclusion in the next iteration of the physics engine.
The parameters of the plugin are configured via SDF in the model file. The next table summarizes all the available SDF parameters.
| Parameter | Description |
|---|---|
| <xDotU> | Added mass in surge |
| <yDotV> | Added mass in sway |
| <zDotW> | Added mass in heave |
| <kDotP> | Added mass in roll |
| <mDotQ> | Added mass in pitch |
| <nDotR> | Added mass in yaw |
| <xUabsU> | Quadratic drag in surge |
| <xU> | Linear drag in surge |
| <yVabsV> | Quadratic drag in sway |
| <yV> | Linear drag in sway |
| <zWabsW> | Quadratic drag in heave |
| <zW> | Linear drag in heave |
| <kPabsP> | Quadratic drag in roll |
| <kP> | Linear drag in roll |
| <mQabsQ> | Quadratic drag in pitch |
| <mQ> | Linear drag in pitch |
| <nRabsR> | Quadratic drag in yaw |
| <nR> | Linear drag in yaw |
| <default_current> | Default ocean current vector |
Note about added mass: SDFormat also supports added mass natively. Until we deprecate the added mass parameters of this plugin, do not set the added mass parameters in both places, choose one (either in this plugin or under <inertial> of your link).
A simple example
Let's download the provided buoyant_cylinder.sdf world and run to see an example of a cylinder with three plugins attached:
- Buoyancy: It will make the cylinder float on the surface of the water.
- Hydrodynamics: It will simulate the damping generated by the fluid surrounding the cylinder.
- Trajectory follower: It will apply some force to move the cylinder one meter in the positive
Xdirection.
Observe how the cylinder does not sink, and slowly makes its way until it reaches (1, 0, 0) in world coordinates.
Now let's make a change in the hydrodynamics parameters. Considering that the model only moves in X direction (or surge in the maritime terminology), we're going to reduce the value of <xUabsU> and <xU> parameters. Update these parameters to:
And run Gazebo again:
Notice how the vehicle does not stop at the 1 meter mark. Instead, the cylinder stops further. This is because we lowered the linear and quadratic drag in the direction that the model is moving.
Let's now try the opposite. Go ahead and update the same parameters to the following values:
And run Gazebo:
See how slow the cylinder moves. With these set of parameters we increased the damping in the surge axis, causing the vehicle to slowly move towards its goal.
Experimental - How to tune the parameters
The hydrodynamics plugin requires a large number of parameters to model the added mass and drag behaviors of underwater vehicles. This section describes a method to generate an initial set of parameters for the hydrodynamics plugin. Note these parameters need to be tested and possibly tweaked to guarantee model stability.
Added mass
A python library called Capytaine can be used to determine the added mass matrix of your vehicle. Capytaine enables the user to import a mesh (.stl), define a set of linear potential flow problems and solve these using the included Boundary Element Method (BEM) solver.
Capytaine is typically used to model the interaction between floating bodies and waves, however it can be applied to ROVs by setting the wave frequency and free surface both to infinity (this assumes that the added mass is approximately constant since the ROV does not operate near the wave zone and that it operates in infinitely deep water respectively) 1, 2.
Furthermore, it is recommended to use a simplified mesh when computing the added mass with Capytaine, since a complex mesh is computationally prohibitive.
Linear and quadratic damping
Computing the linear and quadratic damping coefficients is generally not possible using computational analysis and is usually done experimentally 1. If determining the damping coefficients experimentally is not feasible, the same method described by Berg2012 can be used to estimate these values from a similar ROV 1.
References
[1] BERG, V. Development and Commissioning of a DP system for ROV SF 30k, 2012.
[2] FOSSEN , T. I. Lecture notes: Ttk 4190 guidance, navigation and control of vehicles, February 2021.
[3] BINGHAM, B. et al., Toward Maritime Robotic Simulation in Gazebo, Oceans Conference, 2019.